题目描述

某条流水线上，有 n 个置物平台和 n 条传送带。

每条传送带连接着两个置物平台。例如，传动带连接 A→B ，表示传送带将平台 A 的物品运送到平台 B ，并且称该传送带为 A 的 “出口传送带” ，B 的 “进口传送带” 。

同时，每条传送带有一个传送时间，表示物体从传送带一段传送到另一端所需的时间。

已知在该流水线上，每个置物平台有且仅有一条 “出口传动带” ，但可能有多条 “进口传送带” 。

为了调试该流水线，你把一个物体放在了某个置物平台上，物体会顺着传送带的方向不断运动。

你想知道，经过多长时间物体会被传送回起点平台，或者永远无法回到起点。

输入

输入包含多组数据。

第一行包括一个整数 T(1≤T≤100) ，表示数据组数。

接下来的每组数据，第一行包括一个整数 n(1≤n≤103) ，表示置物平台的个数。

接下来 n 行，第 i 行包含两个整数 di,ti(1≤di≤n,1≤ti≤109) ，表示一条传送带连接 i→di ，即从 i 号置物平台传送到 di 号置物平台，传送时间为 ti 。

输出

对于每组数据，输出一行，一行包括 n 个整数 。

第 i 个整数表示将物体放到 i 号置物平台后，经过多长时间，物体将返回起点。如果物体永远不能返回起点，输出 −1 。

输入样例

3
6
2 1
3 1
1 4
1 5
2 1
2 4
2
1 1919
1 810
2
1 1919
2 810

输出样例

6 6 6 -1 -1 -1
1919 -1
1919 810

样例解释

第一组数据的情况如下： 

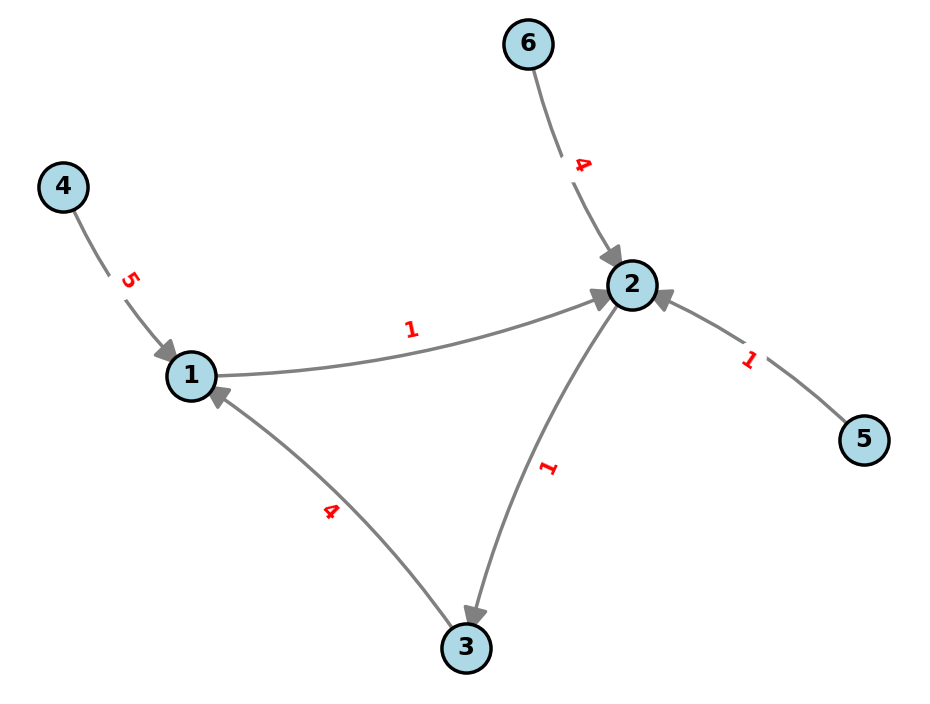
当物体放在 1 号平台上，运动路径为 1→2→3→1 ，传送时间为 1+1+4=6 。

当物体放在 2 号平台上，运动路径为 2→3→1→2 ，传送时间为 1+4+1=6 。

当物体放在 3 号平台上，运动路径为 3→1→2→3 ，传送时间为 4+1+1=6 。

当物体放在 4,5,6 号平台上，均无法回到起点。

题解

#include<stdio.h>
int plat[1001][2], num = 0/用于标记递归入口/;
long long sum = 0/总用时/, rt = 0/某次循环时函数的调用次数/;
int n;
long long time(int i)
{
	if (rt > n)//递归次数不可能超过平台总数，如果超过了，说明无法回到初始位置
	{
		sum = 0;
		num = 0;
		rt = 0;//这里在退出递归循环时，重置使用过的全局变量
		return -1;
	}
	if (num == i)//此时函数回到初始位置
	{
		long long res = sum;
		rt = 0;
		sum = 0;
		num = 0;
		return res;
	}
	if (num == 0)
	{
		num = i;
	}//入口：这里可以理解为一个循环，如果本次调用该函数是第一次，那么标记初始位置，直到回到该位置（因为平台编号不为0）
	rt++;
	sum += plat[i][1];
	return time(plat[i][0]);//利用递归
}
int main()
{
	int T;
	scanf("%d", &T);
	for (int i = 0; i < T; i++)
	{

		scanf("%d", &n);
		for (int j = 1; j <= n; j++)
		{
			scanf("%d%d", &plat[j][0], &plat[j][1]);
		}
		for (int j = 1; j <= n; j++)
		{
			printf("%lld ", time(j));
		}
		printf( "\n" );
	}
        return 0;
}