题目背景

如果你了解什么是 PID 控制系统，请直接看一句话题面

夜深人静的实验室里，奇迹正在调试着使用 PID 系统控制的小车。苦恼于手动调参数却无法直观地看到系统的响应，奇迹想请你帮他编写一个模拟 PID 控制系统输出的程序。

《自动控制原理》是很多学院的必修课，与如今的工程实际密切联系。有一种经典的控制方法被称为PID控制，即比例(Proportion)-积分(Integration)-微分(Differential)控制算法，它接受一个输入信号，通过对输入信号与输出信号的差值，即误差进行运算，并以此控制输出信号。

在本题中，我们设输入信号为固定值 Ui, 输出信号 Uo 初始时刻为零；通过对误差的比例与微分运算，更新输出信号的值。具体的系统方框图如下：

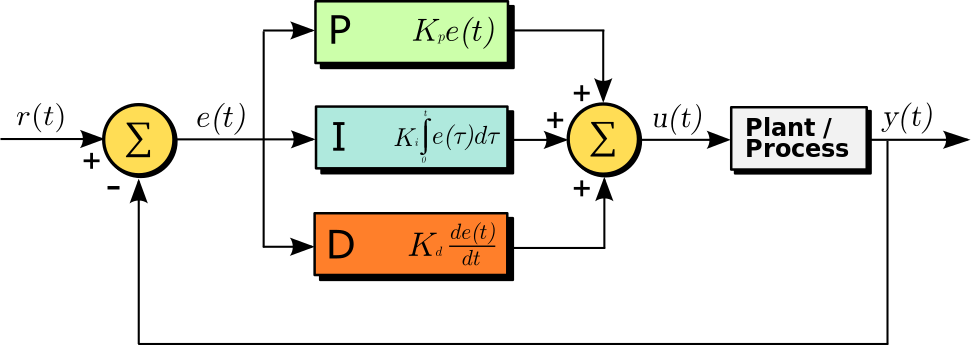
具体而言，为了把问题写成可迭代的离散模拟、便于编程实现，下面给出常用且明确的离散化约定：

• 用下标 k 表示离散时刻，初始时刻取为 k=0，且初值 Uo[0]=0。
• 误差在第 k 步定义为使用上一时刻的输出计算：e[k]=Ui−Uo[k−1].这样在计算第 k 步时所需的量均为已知值（避免出现等式左右同时包含 Uo[k] 的隐式情况）。
• 积分（累加）项取包含当前误差：S[k]=S[k−1]+e[k]，初值 S[0]=e[0]=Ui−Uo[0]=Ui。
• 微分项采用差分：Δe[k]=e[k]−e[k−1]。
• 按上述定义，第 k 步的输出为：Uo[k]=kp⋅e[k]+kd⋅(e[k]−e[k−1])+ki⋅S[k]

按此迭代规则，从 k=1 到 k=t（共 t 步）依次计算并输出每个时刻的输出信号值即可（每行输出一个浮点数，保留三位小数）。

举例说明：若 Ui=10，且已知上一时刻 Uo(t−1)=6.5，则当前误差 e(t)=10−6.5=3.5；若累加和为 48，误差差分为 3.5−4.5=−1，则按上式计算得到

Uo(t)=3.5kp+(−1)kd+48ki.

题目描述（一句话）

给定阶跃信号 Ui，以及 PID 控制参数 kp,ki,kd，模拟并输出零初始条件系统在 t 个时刻的输出信号值。

输入

第一行四个浮点数 ui,kp,ki,kd

第二行一个整数 t，代表模拟总时刻数。保证 1≤t≤103。

输出

共 t 行，每行一个浮点数，代表当前时刻的输出信号值，保留三位小数。

输入样例

10 0.1 0.005 0.01
1000

输出样例

1.050
0.979
1.043
1.080
...
9.903
9.903
9.904
9.904
9.904

Hint

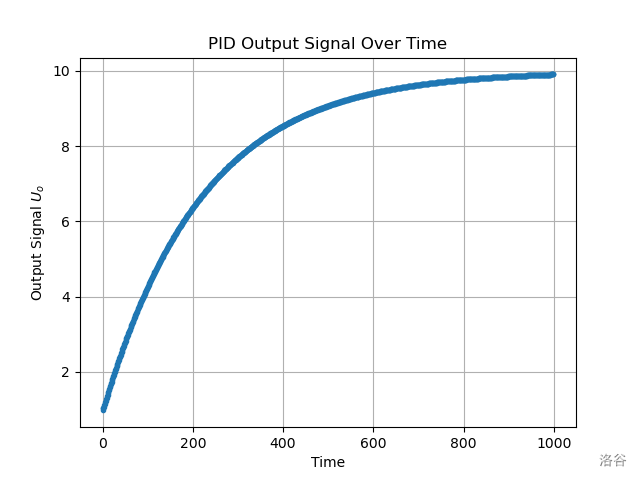
样例输出的图像如下：